はじめに
こんにちは、野村です。
今回は、python3で数列を吐き出すスクリプトを紹介します。
スクリプトを書くにあたって以下のルールを設けています。
・ループ(whileやfor)を使わない。
・内包表記のforは使っていい。
素数
・1より大きい自然数で、正の約数が1と自分自身のみである数。
import math
def sosu(a):
if a[0] > math.sqrt(a[-1]): return a
return [a[0]] + sosu([x for x in a[1:] if x%a[0]!=0])
print(sosu(list(range(2,100)))) # 100未満の素数を表示
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]
双子素数
・双子素数:差が2である2つの素数の組
・いとこ素数:差が4である2つの素数の組
・セクシー素数:差が6である2つの素数の組
from functools import reduce
from math import sqrt
def loop(a, i, f):
b = len([x for x in [y for y in a if y<=sqrt(i)] if i%x==0])==0
if b:
a=a+[i]
if (i-f) in a : return a
return loop(a,i+1,f)
def lam(a,f):
b = loop(a[0], a[0][-1]+1, f)
return [b, a[1]+[b[-1]]]
def sosu(f,c):
return [[x-f,x] for x in reduce(lam, [f for i in range(c)], [[2],[]])[1]]
print(sosu(2,10)) # 双子素数を10組表示
print(sosu(4,10)) # いとこ素数を10組表示
print(sosu(6,10)) # セクシー素数を10組表示
[[3, 5], [5, 7], [11, 13], [17, 19], [29, 31], [41, 43], [59, 61], [71, 73], [101, 103], [107, 109]] [[3, 7], [7, 11], [13, 17], [19, 23], [37, 41], [43, 47], [67, 71], [79, 83], [97, 101], [103, 107]] [[5, 11], [7, 13], [11, 17], [13, 19], [17, 23], [23, 29], [31, 37], [37, 43], [41, 47], [47, 53]]
幸運数
・ポーランドの数学者スタニスワフ・ウラムによって提案された数列。
・素数の性質を研究するために、素数に似たルールで導き出せる数列を考案したとのこと。
def loop(n,a):
b = [([0]+a)[x] for x in range(0,len(a)+1) if x%a[n]!=0]
return loop(n+1,b) if b[n]<(len(b)+1) else b
def luk(n):
return loop(1, list(range(1,n,2)))
print(luk(100)) # 100未満の幸運数を表示
[1, 3, 7, 9, 13, 15, 21, 25, 31, 33, 37, 43, 49, 51, 63, 67, 69, 73, 75, 79, 87, 93, 99]
階乗
・1 から n までのすべての整数の積。
def fact(n):
return 1 if n<2 else n * fact(n-1)
print([fact(n) for n in range(10)]) # 階乗を10個表示
[1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880]
フィボナッチ数
・イタリアの数学者レオナルド・フィボナッチにちなんで名付けられた数
### 再帰を使う方法
def fibo(n):
return n if n<2 else fibo(n-1)+fibo(n-2)
print([fibo(i) for i in range(10)]) # フィボナッチ数を10個表示
### 関数を使う方法
def f(n):
if n<2: return n
n -= 1
return (4 << n*(3+n)) // ((4 << 2*n) - (2 << n)-1) & ((2 << n)-1)
print([f(n) for n in range(10)]) # フィボナッチ数を10個表示
### 行列を使う方法
import numpy
def fib(n):
if n<1: return 0
n -= 1
m = numpy.matrix('1 1 ; 1 0') ** n
return m.item(0)
print([fib(n) for n in range(10)]) # フィボナッチ数を10個表示
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34] [0, 1, 1, 2, 3, 5, 8, 13, 21, 34] [0, 1, 1, 2, 3, 5, 8, 13, 21, 34]
パスカルの三角形
・二項展開における係数を三角形状に並べたもの。
def pas(n):
if n<1 : return [1]
p = pas(n-1)
return list(map(lambda a,b:a+b, [0]+p, p+[0]))
print([pas(x) for x in range(10)]) # パスカルの三角形を10段表示
[[1], [1, 1], [1, 2, 1], [1, 3, 3, 1], [1, 4, 6, 4, 1], [1, 5, 10, 10, 5, 1], [1, 6, 1 5, 20, 15, 6, 1], [1, 7, 21, 35, 35, 21, 7, 1], [1, 8, 28, 56, 70, 56, 28, 8, 1], [1, 9, 36, 84, 126, 126, 84, 36, 9, 1]]
内包表記で書いてみた
mapを使うともう少し短くなるのだけど、ソースが消えてしまっていた。
そのうちmapを使って書き直してみます。
>>> [(x.append([0]+[x[i][y]+x[i][y+1] for y in range(len(x[i])-1)]+[0]),x[i])[1][1:- 1] for x in [[[0,1,0]]] for i in range(10)]
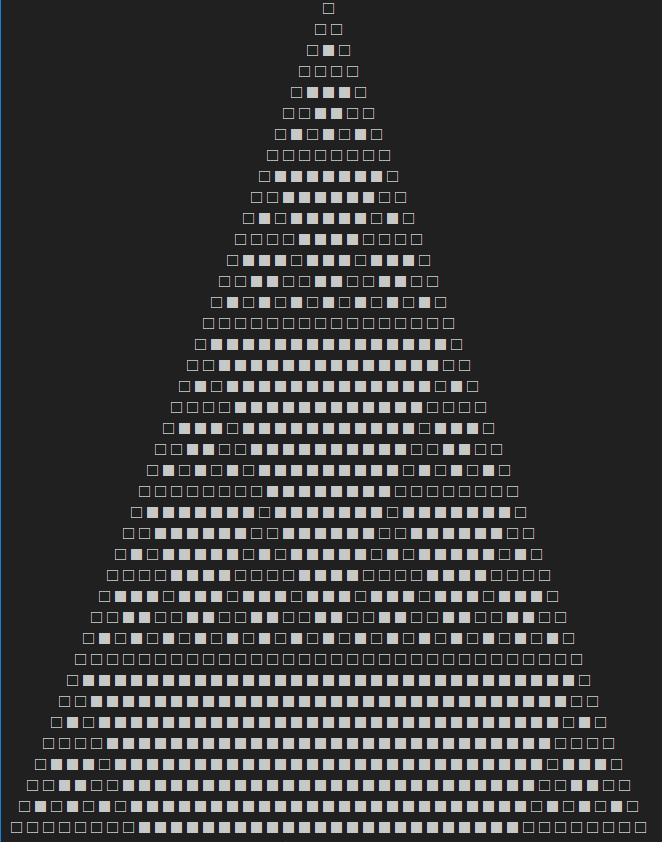
おまけ:三角形を書いてみた
パスカルの三角形を三角形に配置して奇数を□、偶数を■に置き換えるとこうなります。
このスクリプトにはwhileもforも変数の再代入も使ってます。すいません。
def pas():
a = [1]
while 1:
yield a
a = [0]+a+[0]
a = [a[i-1]+a[i] for i in range(1,len(a))]
p = pas()
for i in range(40):
str = ""
for k in range(40-i):
str += " "
for j in next(p):
str += "■" if j%2==0 else "□"
print(str)
最後に
今回の記事は、以前運営していたサイト(現在は消滅)に公開していたものを再編成したものです。
python3以外に、javascript, ruby, php7, scala, haskell, lisp, c++, java8, c# でも同じような記事を公開していたのですよ。
ソースは残っているので、気が向いたら今回のように再編成して公開するかも。
というわけで、今回はこれにて。